Perfiles de fuerza / velocidad individualizados: consideraciones de aplicación para aumentar la precisión de la predicción

Los perfiles de fuerza/velocidad individualizados se utilizan comúnmente para predecir el 1RM. Sin embargo, los resultados son mixtos: algunos estudios demuestran que pueden predecir con precisión 1RM; sin embargo, otros estudios revelan lo contrario. Acompáñame a comentar cuáles son las características individuales que deben considerarse para llevar a la práctica aumentando la precisión de la predicción de 1RM.

Puntos claves

1. Las ecuaciones de regresión lineal individualizada son los perfiles de velocidad más comunes utilizados para predecir 1RM
2. Los hallazgos generales de la literatura son mixtos en cuanto a la precisión de la predicción de 1RM
3. Hay varias consideraciones de aplicación para aumentar la precisión de la predicción de 1RM

 

Cuando alguien dice, «Entrenamiento basado en la velocidad» lo que típicamente viene a la mente para la mayoría de los individuos es el perfil de carga y velocidad. Luego, la mayoría típicamente piensan en un perfil de carga-velocidad como una ecuación de regresión que involucra velocidad en el eje x y carga en el eje y con una extrapolación de la velocidad para predecir 1RM. Las ecuaciones de regresión se utilizan típicamente para predecir 1RM con el fin de monitorear 1RM a lo largo del tiempo o como un método en el que basar la prescripción de la sesión de entrenamiento. Hay innumerables estudios que incluyen perfiles de carga y velocidad de la ecuación de regresión; por lo tanto, en lugar de abordar todos y cada uno de los estudios, esta breve reseña ofrecerá una breve instantánea de las consideraciones más importantes y consideraciones  para aumentar la precisión de la predicción de 1RM.    

En resumen, estos estudios investigan la validez y/o fiabilidad de los perfiles de fuerza/velocidad para la predicción de 1RM. La validez se refiere a la exactitud de los métodos de predicción de 1RM. La fiabilidad se refiere a la consistencia de los métodos de predicción de 1RM. Es importante investigar tanto la validez como la fiabilidad, ya que un método de predicción de 1RM puede ser inválido (no predecir con exactitud 1RM), pero puede seguir siendo fiable, lo que significa que constantemente sobre o predecir por debajo 1RM por una magnitud específica. Por ejemplo, digamos que un método particular de predicción de 1RM predice consistentemente un exceso de 1RM en 10 kilos. Aunque no es válido (sobre-predice 1RM en 10 kilos), es fiable (sobre-predice consistentemente 1RM en 10 kilos). Por lo tanto, en este ejemplo en particular, este individuo todavía podría usar esto como un método sólido para predecir el 1RM simplemente sabiendo que su 1RM es siempre ~10 kilos menos que la predicción real.  

Personalmente, he jugado tanto con ecuaciones de regresión lineal como con ecuaciones de regresión polinómica una buena cantidad para predecir 1RM. Para mí, ambos métodos tienden a sobre-predicar 1RM sustancialmente, lo que es consistente con lo que se reporta en la mayoría de la literatura. Por esta razón, sugiero típicamente el uso de lo que he llamado una Tabla de Velocidad de Primera Reparación Individualizada para cruzar la velocidad de primera reparación individualizada con el porcentaje individualizado de 1RM para la determinación exacta del porcentaje de 1RM en la barra y para la predicción exacta de 1RM. Sin embargo, para algunos individuos he encontrado que los perfiles de velocidad de carga de la ecuación de regresión típica son capaces de predecir 1RM con una precisión razonablemente buena, por lo que todavía creo que vale la pena discutirlos. Simplemente ten en cuenta las importantes consideraciones que se ilustran a continuación si estás interesado en darles una oportunidad.

 

¿Cuál es la mejor métrica de velocidad a utilizar?

Hay varias métricas de velocidad que pueden usarse para predecir 1RM: velocidad concéntrica media (ACV), velocidad media propulsiva (MPV), velocidad máxima (PV), y muchas otras (1). La VCA es la velocidad media durante toda la porción concéntrica del ascenso (es decir, durante la porción en la que se asciende o se «mueve hacia arriba» en la sentadilla o la press de banca). VMP es la velocidad media desde el inicio de la porción concéntrica del levantamiento hasta el punto en que la aceleración de la barra es menor que la aceleración de la gravedad (esto puede ser particularmente útil para evaluar la tasa de desarrollo de la fuerza; también se conoce comúnmente como RFD). PV es la velocidad pico (por lo tanto, máxima) que se alcanza durante la porción concéntrica del levantamiento. 

En un estudio muy reciente en el que se investigaba qué métrica de velocidad podía determinar la carga relativa de la press de banca con la mayor fiabilidad, la ACV tenía el mayor coeficiente de correlación persa (R = 0,993) y el menor error estándar de la estimación (VER = 5,11 – 6,03%) (1). El valor R mide la fuerza de la relación entre dos variables (carga y velocidad en este caso concreto) y oscila entre -1,00 y +1,00 (un valor absoluto de 1,00 indicaría que existe una correlación perfecta entre carga y velocidad). El SEE representa la exactitud e ilustra la variación alrededor de una línea de regresión (por lo que cuanto menor sea el SEE, menor será la varianza y mayor la exactitud de la predicción). 

¿Cuál es el mejor tipo de método de predicción de 1RM a utilizar?

Hay tres métodos primarios de predicción de 1RM que utilizan la velocidad y que se emplean actualmente en la literatura científica: umbral de velocidad mínima (MVT), carga a velocidad cero (LD0) y fuerza-velocidad (FV) (2). El MVT sugiere que la repetición final antes del fallo es siempre en el mismo ACV. Por lo tanto, el método MVT implica resolver la ecuación de regresión lineal para y (1RM) con el MVT (x). El método LD0 es idéntico al método MVT; sin embargo, implica la resolución de la ecuación lineal, ecuación de regresión para una velocidad de 0 m.s-1, en lugar de la MVT. El método FV implica la identificación de la intercepción entre FV y la relación peso-velocidad (en este caso el peso se determina multiplicando cada una de las cargas absolutas por la aceleración estándar debida a la gravedad o 9,81 m.s-1). En conclusión, se ha demostrado que el método de predicción del MVT 1RM es el más válido y fiable de los tres métodos mencionados (2). 

 

Ecuaciones de regresión lineal individual frente a ecuaciones de regresión lineal de grupo

No debería sorprender que las ecuaciones de regresión lineal individual sean más precisas para predecir 1RM que las ecuaciones de regresión lineal de grupo (3), ya que se ha establecido que la relación entre carga y velocidad debe ser individualizada (4). No veo el propósito de investigar las ecuaciones de regresión lineal grupal, ni tampoco veo la eficacia de las ecuaciones de regresión lineal grupal en entornos grupales. En entornos grupales, incluso si varios atletas utilizan el mismo dispositivo de VBT, cada uno de ellos puede seguir teniendo su ecuación de regresión lineal individual (que depende de la sesión, ya que la ecuación cambiará, por supuesto, cada sesión dependiendo de la carga exacta y la velocidad exacta correspondiente). Por supuesto, utiliza tu propio perfil individualizado de velocidad de carga; no utilice un perfil genérico de velocidad de carga de grupo.  

Velocidad máxima prevista vs. no velocidad máxima prevista

Creo que una limitación importante de la mayoría de los estudios es que casi nunca se proporciona un taco de velocidad máxima prevista. Sin embargo, en un estudio en el que había una condición que recibía un taco de velocidad máxima prevista y una condición de control (no se recibió ningún taco de velocidad máxima prevista), la predicción de 1RM fue ligeramente más precisa en la condición que recibía un taco de velocidad máxima prevista (errores absolutos: 3,1 ± 2,3 frente a 4,1 ± 1,9 kg) (5). De nuevo, lógicamente esto no debería sorprender, porque si a un sujeto no se le proporciona un taco para levantar cada repetición con la máxima velocidad prevista, ciertas repeticiones pueden ser más rápidas que las normales y ciertas repeticiones pueden ser más lentas que las normales. En consecuencia, esto tendrá cambios drásticos en la pendiente de la línea de regresión; por lo tanto, influyendo en la predicción de 1RM. 

Levantadores experimentados vs. inexpertos

Curiosamente, Banyard y otros (2017) informaron de que los estados de entrenamiento más duros (sujetos capaces de ponerse en cuclillas con peso libre 1,5 veces la masa corporal) tenían predicciones más precisas de 1RM que los estados de entrenamiento más bajos (6). Los autores no proporcionaron ninguna discusión o interpretación para explicar estos hallazgos. No estoy del todo seguro de por qué es así, ya que he sido testigo de resultados contradictorios con los de los «estados de entrenamiento más duros». Para especular, puede ser porque los «estados de entrenamiento superiores» pueden «moler» (es decir, realizar repeticiones a velocidades más lentas); sin embargo, dado que la ecuación de regresión lineal individualizada tiene en cuenta el VCA de 1RM de un individuo, esto no explica todo el panorama.  

Ejercicios de peso libre vs. ejercicios basados en máquinas

Por último, llegamos a los ejercicios de peso libre frente a los de máquina. Aquí es donde las diferencias en los hallazgos realmente empiezan a entrar en juego. En su mayor parte, las ecuaciones de regresión lineal que implican ejercicios de peso libre no son válidas (6, 7) ni fiables (6), y típicamente sobreestiman el 1RM real en una magnitud significativa (6, 7). Sin embargo, en su mayor parte, las ecuaciones de regresión lineal que implican ejercicios basados en máquinas son típicamente razonablemente válidas y confiables para la predicción de 1RM (5, 8). No estoy del todo seguro de por qué los ejercicios basados en máquinas son típicamente más precisos, pero para especular creo que puede ser porque los ejercicios de peso libre son más propensos a las desviaciones técnicas; por lo tanto, la trayectoria distintiva de la barra puede jugar un papel.

Alto porcentaje de 1RM vs. Bajo porcentaje de 1RM

Las ecuaciones de regresión lineal que utilizan un porcentaje mayor de 1RM (~80% de 1RM) son más precisas que las que utilizan un porcentaje menor de 1RM (~60% de 1RM), sin importar el número de puntos de datos involucrados en la ecuación de regresión lineal (6, 7). Por lo tanto, parece que la relación entre la carga y la velocidad se vuelve curva (en lugar de lineal) a medida que la carga en la barra aumenta. En mi opinión, la relación carga-velocidad se parece más a una ecuación de regresión polinómica de segundo orden que a una ecuación de regresión lineal. 

Ecuaciones de regresión lineal individualizada vs. ecuaciones de regresión polinómica individualizada

Yo diría con cautela que las ecuaciones de regresión polinómica pueden ser más precisas que las de regresión lineal para predecir 1RM (9), pero lamentablemente hay muy pocas investigaciones sobre su eficacia. En realidad me sorprende que sea así, ya que el componente que más tiempo consume para realizar un estudio es típicamente la recolección de datos. En otras palabras, los investigadores ya tienen los datos, por lo que sólo es cuestión de ejecutar las estadísticas, informar de los resultados e integrar los resultados en la sección de discusión del documento. De hecho, el documento más reciente sobre la prescripción de carga autorregulada utilizó un método interesante para prescribir la carga utilizando una ecuación de regresión polinómica (10).

 

 

Conclusión

En resumen, si está interesado en probar las ecuaciones de regresión, debe utilizar una ecuación individualizada (pruebe tanto lineal como polinómica), ACV como la métrica de la velocidad una señal de velocidad máxima prevista y un alto porcentaje de 1RM. Además, la predicción puede ser más precisa si se tiene un estado de entrenamiento más alto y se utiliza para un ejercicio basado en la máquina (lo que probablemente es poco frecuente). En el cuadro 1 se ilustra un resumen de las consideraciones prácticas. 

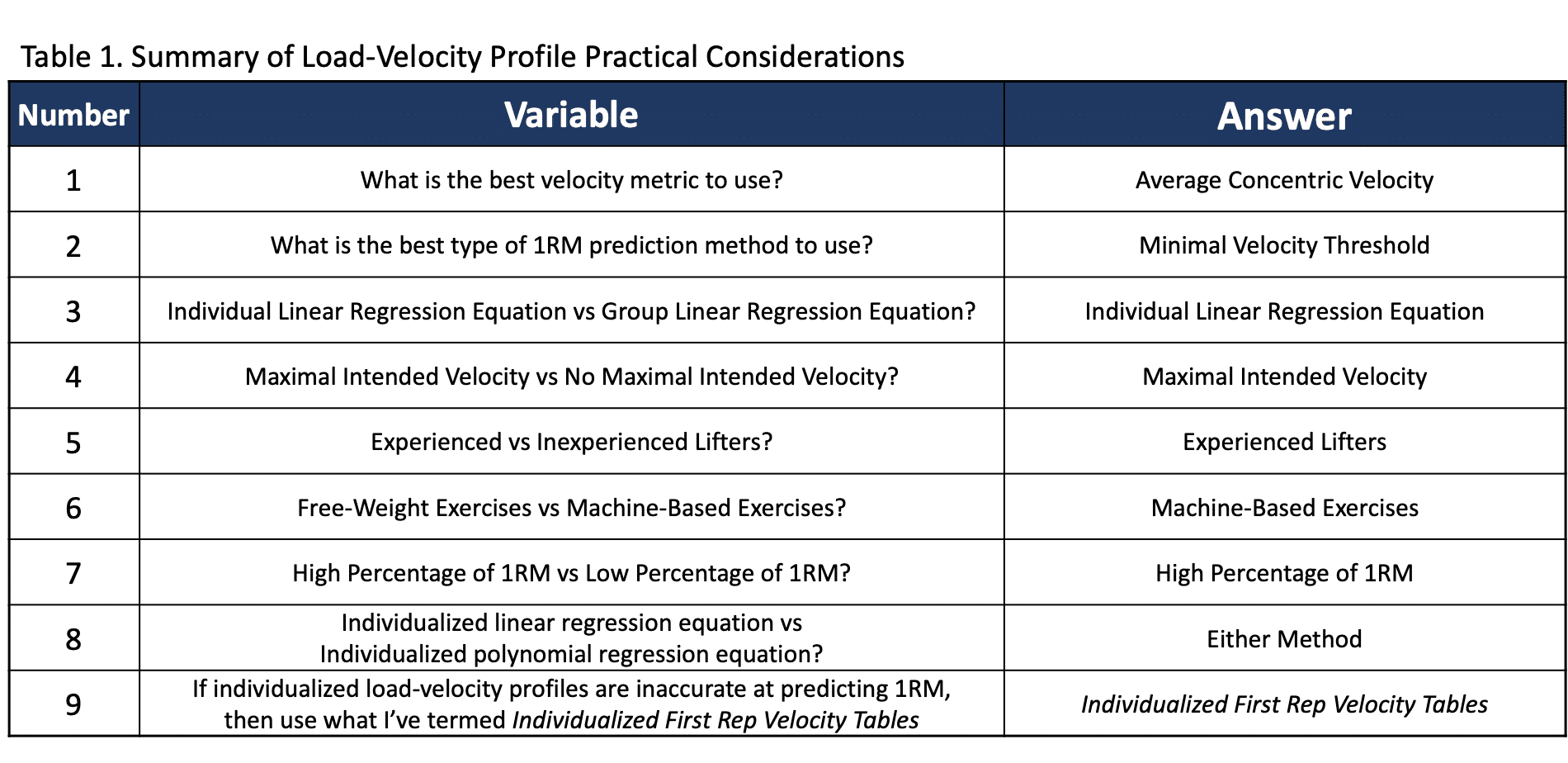
Pero una última pregunta puede ser: «En la literatura, ¿cuán precisos son los perfiles de velocidad de carga en la predicción de 1RM?» Algunos son casi perfectos (5, 8), mientras que otros sobre-predicen 1RM hasta ~ 25 kilos (6, 7), pero es en gran medida variable inter individualmente. Sin embargo, la buena noticia es que la velocidad es fiable en cada porcentaje de 1RM (11). Por lo tanto, típicamente sugiero usar lo que he llamado una Tabla de Velocidad de Primera Reparación Individualizada y cruzar la velocidad con el porcentaje de 1RM. Como nota final, personalmente creo que la predicción de 1RM es más útil como herramienta para monitorizar 1RM en el tiempo que como un método real para prescribir TODO el período de sesiones, simplemente porque otras estrategias de autorregulación pueden prescribir y autorregular apropiadamente la carga y el volumen. El próximo artículo abordará los métodos de predicción y monitoreo de 1RM que he encontrado efectivos usando la Tabla Individualizada de Primera Velocidad de Repetición que he creado. 

Puntos clave

1. Las consideraciones de aplicación para los perfiles de velocidad de carga incluyen el uso de una ecuación individual, la velocidad concéntrica media, el umbral de velocidad mínima, la velocidad máxima prevista y un alto porcentaje de 1RM
2. Emplea ecuaciones de regresión lineal individualizada o ecuaciones polinómicas individualizadas de segundo orden sólo si son consistentemente precisas para predecir 1RM para ti. 
3. Emplee lo que he llamado una Tabla de Velocidad de Primera Reparación Individualizada para cruzar la velocidad de primera reparación individualizada con el porcentaje individualizado de 1RM como un método rápido y fácil para determinar con precisión el porcentaje de 1RM en la barra y predecir 1RM

 

Bibliografía

1. Garcia-Ramos, A, Pestana-Melero, FL, Perez-Castilla, A, Rojas, FJ, and Haff, GG. Mean velocity vs. mean propulsive velocity vs. peak velocity: which variable determines bench press relative load with higher reliability. The Journal of Strength and Conditioning Research 32(5), 1273 – 1279, 2018.
2. Hughes, LJ, Banyard HG, Dempsey, AR, and Scott, BR. Using a load-velocity relationship to predict one repetition maximum in free-weight exercise: a comparison of the different methods. The Journal of Strength and Conditioning Research 33(9), 2409 – 2419, 2019.
3. Benavides-Ubric, A, Diez-Fernandez, DM, Rodriguez-Perez, MA, Ortega-Becerra, M, and Pareja-Blanco, F. Analysis of the load-velocity relationship in deadlift exercise. Journal of Sports Science and Medicine 19, 452 – 459, 2020.
4. Helms, ER, Storey, AG, Cross, MR, Brown, SR, Lenetsky, S, Ramsay, H, Dillen, C, and Zourdos, MC. RPE and velocity relationships for the back squat, bench press, and deadlift in powerlifters. The Journal of Strength and Conditioning Research 31(2): 292 – 297, 2017.
5. Jimenez-Alonso, A, Garcia-Ramos, A, Cepero, M, Miras-Moreno, S, Rojas, FJ, and Perez-Castilla. Velocity performance feedback during the free-weight bench press testing procedure: an effective strategy to increase the reliability and one repetition maximum accuracy prediction. The Journal of Strength and Conditioning Research [Epub ahead of print], 2020.
6. Banyard, HG, Nosaka, K, and Haff, GG. Reliability and validity of the load-velocity relationship to predict the 1RM back squat. The Journal of Strength and Conditioning Research 31(7), 1897 – 1904, 2017.
7. Ruf, L, Chery, C, and Taylor K. Validity and reliability of the load-velocity relationship to predict the one-repetition maximum in deadlift. The Journal of Strength and Conditioning Research 32(3), 681 – 689, 2018.
8. Perez-Castilla, A, Suzovic, D, Domanovic, A, Fernandes, JFT, and Garcia-Ramos, A. Validity of different velocity-based methods and repetitions-to-failure equations for predicting the 1 repetition maximum during 2 upper-body pulling exercises. The Journal of Strength and Conditioning Research [Epub ahead of print], 2019.
9. Pestana-Melero, FL, Haff, GG, Rojas, FJ, Perez-Castilla, A, and Garcia-Ramos, A. Reliability of the load-velocity relationship obtained through linear and polynomial regression models to predict the 1-repetition maximum load. Journal of Applied Biomechanics 34(3), 184 – 190.
10. Dorrell, HF, Moore, JM, and Gee, TI. Comparison of individual and group-based load-velocity profiling as a means to dictate training load over a 6-week strength and power intervention. Journal of Sports Sciences [Epub ahead of print].
11. Banyard, HG, Nosaka, K, Vernon, AD, and Haff, GG. The reliability of individualized load-velocity profiles. International Journal of Sports Physiology and Performance 13(6), 763 – 769.