Profili di velocità di prestito personalizzati: Considerazioni sull’applicazione per aumentare l’accuratezza della previsione

I profili di carico-velocità personalizzati vengono comunemente impiegati per prevedere il 1RM. Nonostante ciò, i risultati sono contrastanti: alcuni studi dimostrano che possono prevedere accuratamente il 1RM; tuttavia, altri studi rivelano il contrario. Unisciti a me mentre affronto quali sono le sottigliezze individuali che devono essere considerate per l’applicazione al fine di aumentare la precisione della previsione 1RM.

 

Points clés

1. Le equazioni di regressione lineare individualizzate sono i profili di carico-velocità più comunemente impiegati per prevedere il 1RM
2. I risultati complessivi della letteratura sono misti in termini di accuratezza della previsione del 1RM
3. Ci sono diverse considerazioni applicative al fine di aumentare l’accuratezza della previsione del 1RM

Quando qualcuno dice “Formazione basata sulla velocità”, ciò che viene in mente per la maggior parte delle persone è il profilo di carico-velocità. Successivamente, la maggior parte delle persone pensa tipicamente a un profilo di carico-velocità come a una equazione di regressione che coinvolge la velocità sull’asse x e il carico sull’asse y con un’estrapolazione della velocità al fine di prevedere 1RM. Le equazioni di regressione vengono tipicamente utilizzate per prevedere 1RM al fine di monitorare 1RM nel tempo o come metodo in base al quale prescrivere la sessione di allenamento. Ci sono innumerevoli studi che coinvolgono profili di carico-velocità delle equazioni di regressione; pertanto, piuttosto che affrontare ogni singolo studio, questa breve recensione fornirà un breve riepilogo delle considerazioni più importanti e delle sottigliezze individuali al fine di aumentare l’accuratezza della previsione di 1RM.

In sintesi, questi studi indagano la validità e/o la attendibilità dei profili di carico-velocità per la previsione del 1RM. La validità si riferisce all’accuratezza dei metodi di previsione del 1RM. La attendibilità si riferisce alla coerenza dei metodi di previsione del 1RM. È importante indagare sia la validità che la attendibilità, poiché un metodo di previsione del 1RM può essere invalido (non predire accuratamente il 1RM), ma può comunque essere attendibile, il che significa che sovrastima o sottostima costantemente il 1RM di una certa entità. Ad esempio, supponiamo che un particolare metodo di previsione del 1RM sovrastimi costantemente il 1RM di 10 chilogrammi. Anche se è invalido (sovrastima il 1RM di 10 chilogrammi), è attendibile (sovrastima costantemente il 1RM di 10 chilogrammi). Pertanto, in questo particolare esempio, questa persona potrebbe ancora usare questo come un solido metodo per prevedere il 1RM semplicemente sapendo che il loro 1RM è sempre ~10 chilogrammi in meno della previsione effettiva.

Personalmente, ho giocato con entrambe le equazioni di regressione lineare e polinomiale abbastanza per prevedere 1RM. Per me, entrambi i metodi tendono a sovrastimare notevolmente 1RM, il che è coerente con quanto riportato nella maggior parte della letteratura. Per questo motivo, di solito suggerisco di utilizzare ciò che ho chiamato una tabella di velocità del primo ripetuto individualizzata per fare riferimento alla velocità del primo ripetuto individualizzato con la percentuale individualizzata di 1RM per una determinazione accurata della percentuale di 1RM sulla barra e per una previsione accurata di 1RM. Tuttavia, per alcuni individui ho trovato che i profili di carico-velocità delle equazioni di regressione tipiche sono in grado di prevedere 1RM con una buona accuratezza, quindi penso ancora che valga la pena discuterne. Tieni semplicemente presenti le importanti considerazioni illustrate di seguito se sei interessato a provarlo.

Qual è la migliore metrica di velocità da usare?

Ci sono vari metriche di velocità che possono essere utilizzate per prevedere il 1RM: velocità concentrica media (ACV), velocità propulsiva media (MPV), velocità di picco (PV) e numerosi altri (1). L’ACV è la velocità media durante l’intera porzione concentrica dell’esercizio (cioè durante la parte in cui si sta salendo o “muovendosi verso l’alto” nello squat o nella panca). La MPV è la velocità media dall’inizio della porzione concentrica dell’esercizio fino al punto in cui l’accelerazione della barra è inferiore all’accelerazione di gravità (questo può essere particolarmente utile per valutare la velocità di sviluppo della forza; comunemente noto anche come RFD). La PV è la velocità massima (di picco) che viene raggiunta durante la porzione concentrica dell’esercizio.

In uno studio molto recente che ha indagato quale metrica di velocità potesse determinare il carico relativo della panca con la massima affidabilità, l’ACV ha avuto il coefficiente di correlazione di Pearson più alto (R = 0.993) e l’errore standard della stima più basso (SEE = 5.11 – 6.03%) (1). Il valore R misura la forza della relazione tra due variabili (carico e velocità in questo caso particolare) e va da -1.00 a +1.00 (un valore assoluto di 1.00 indicherebbe che c’è una correlazione perfetta tra carico e velocità). Il SEE rappresenta l’accuratezza e illustra la variazione intorno a una linea di regressione (quindi più basso è il SEE, minore è la varianza e maggiore è l’accuratezza della previsione).

Qual è il miglior metodo di previsione del 1RM da utilizzare?

Attualmente nella letteratura scientifica sono impiegati tre metodi di previsione del 1RM utilizzando la velocità: soglia minima di velocità (MVT), carico a velocità zero (LD0) e forza-velocità (FV) (2). Il MVT suggerisce che l’ultima ripetizione prima del fallimento è sempre alla stessa ACV. Pertanto, il metodo MVT prevede la risoluzione dell’equazione di regressione lineare per y (1RM) con il MVT (x). Il metodo LD0 è identico al metodo MVT; tuttavia, prevede la risoluzione dell’equazione di regressione lineare per una velocità di 0 m.s-1, invece del MVT. Il metodo FV prevede l’identificazione dell’intercetta tra FV e la relazione peso-velocità (in questo caso il peso è determinato moltiplicando ciascuno dei carichi assoluti per l’accelerazione standard dovuta alla gravità o 9,81 m.s-1). In conclusione, il metodo di previsione del 1RM MVT è stato dimostrato essere il più valido e affidabile dei tre metodi sopra menzionati (2).

Equazioni di regressione lineare individuali vs equazioni di regressione lineare di gruppo

Non dovrebbe sorprendere che le equazioni di regressione lineare individuali siano più accurate nella previsione del 1RM rispetto alle equazioni di regressione lineare di gruppo (3), poiché è ben stabilito che la relazione tra carico e velocità deve essere individualizzata (4). Non vedo lo scopo di indagare le equazioni di regressione lineare di gruppo, né vedo l’efficacia delle equazioni di regressione lineare di gruppo in ambienti di gruppo. In ambienti di gruppo, anche se più atleti utilizzano lo stesso dispositivo VBT, ogni singolo atleta può comunque avere la sua equazione di regressione lineare individuale (che è contingente alla sessione; poiché l’equazione cambierà ovviamente ogni sessione a seconda del carico esatto e della velocità corrispondente esatta). Naturalmente, usa il tuo profilo di carico-velocità individualizzato; non usare un profilo di carico-velocità generico di gruppo.

Velocità Intesa Massimale vs Nessuna Velocità Intesa Massimale

Penso che una delle principali limitazioni con la maggior parte degli studi sia che quasi mai viene fornito un segnale di velocità intesa massimale. Tuttavia, in uno studio in cui c’era una condizione che riceveva un segnale di velocità intesa massimale e una condizione di controllo (nessun segnale di velocità intesa massimale è stato ricevuto), la previsione del 1RM è stata leggermente più accurata nella condizione che riceveva un segnale di velocità intesa massimale (errori assoluti: 3,1 ± 2,3 vs 4,1 ± 1,9 kg) (5). Anche in questo caso, logicamente non dovrebbe sorprendere, poiché se un soggetto non viene fornito con un segnale per sollevare ogni ripetizione con velocità intesa massimale, alcune ripetizioni possono essere più veloci del normale e alcune ripetizioni possono essere più lente del normale. Di conseguenza, questo avrà drastici cambiamenti alla pendenza della linea di regressione; influenzando così il 1RM previsto.

Esperti vs Inesperti Sollevatori

Interessantemente, Banyard et al. (2017) hanno riportato che i soggetti con uno stato di allenamento più alto (in grado di effettuare un back squat con pesi liberi pari a 1,5 volte la massa corporea) hanno previsioni di 1RM più accurate rispetto a quelle di uno stato di allenamento più basso (6). Gli autori non hanno fornito alcuna discussione o interpretazione per spiegare questi risultati. Non sono del tutto sicuro del perché ciò sia così, poiché ho osservato risultati misti con quelli di “stati di allenamento più elevati”. Per speculare, potrebbe essere perché “stati di allenamento più elevati” possono “macinare” (cioè eseguire ripetizioni a velocità più lente); tuttavia, poiché l’equazione di regressione lineare individualizzata tiene conto dell’ACV 1RM individuale, ciò non spiega l’intero quadro.

Esercizi con Pesi Liberi vs Esercizi su Macchine

Infine, arriviamo agli esercizi con pesi liberi vs esercizi su macchine. È qui che le differenze nei risultati iniziano davvero a diventare evidenti. Per la maggior parte, le equazioni di regressione lineare che coinvolgono esercizi con pesi liberi non sono valide (6, 7) né affidabili (6) e di solito sopravvalutano di una quantità significativa il 1RM effettivo (6, 7). Tuttavia, per la maggior parte, le equazioni di regressione lineare che coinvolgono esercizi su macchine sono generalmente ragionevolmente valide e affidabili per la previsione del 1RM (5, 8). Non sono del tutto sicuro del perché gli esercizi su macchine siano generalmente più accurati, ma per speculare penso che possa essere perché gli esercizi con pesi liberi sono più soggetti a deviazioni tecniche; quindi, il percorso distinto della barra potrebbe svolgere un ruolo.

Alto percentuale di 1RM vs basso percentuale di 1RM

Le equazioni di regressione lineare che utilizzano una percentuale più alta di 1RM (~80% di 1RM) sono più accurate di quelle che utilizzano una percentuale più bassa di 1RM (~60% di 1RM), indipendentemente dal numero di punti dati coinvolti nell’equazione di regressione lineare (6, 7). Pertanto, sembra che la relazione tra carico e velocità diventi curva (piuttosto che lineare) man mano che il carico sulla barra aumenta. A mio parere, la relazione carico-velocità assomiglia più da vicino a un’equazione di regressione polinomiale di secondo ordine che a un’equazione di regressione lineare.

Equazioni di regressione lineare individualizzate vs equazioni di regressione polinomiali individualizzate

Mi sentirei di argomentare cautamente che le equazioni di regressione polinomiale possono essere più accurate delle equazioni di regressione lineare nel prevedere 1RM (9), ma purtroppo c’è una ricerca molto limitata sulla loro efficacia. Sono effettivamente sorpreso che sia così, poiché la componente più impegnativa nell’esecuzione di uno studio è di solito la raccolta dei dati. In altre parole, i ricercatori hanno già i dati, quindi si tratta solo di eseguire le statistiche, riportare i risultati e integrarli nella sezione discussione della carta. Infatti, l’articolo più recente sulla prescrizione di carico autoregolata ha effettivamente utilizzato un interessante metodo per prescrivere il carico utilizzando un’equazione di regressione polinomiale (10).

 

 

Conclusione

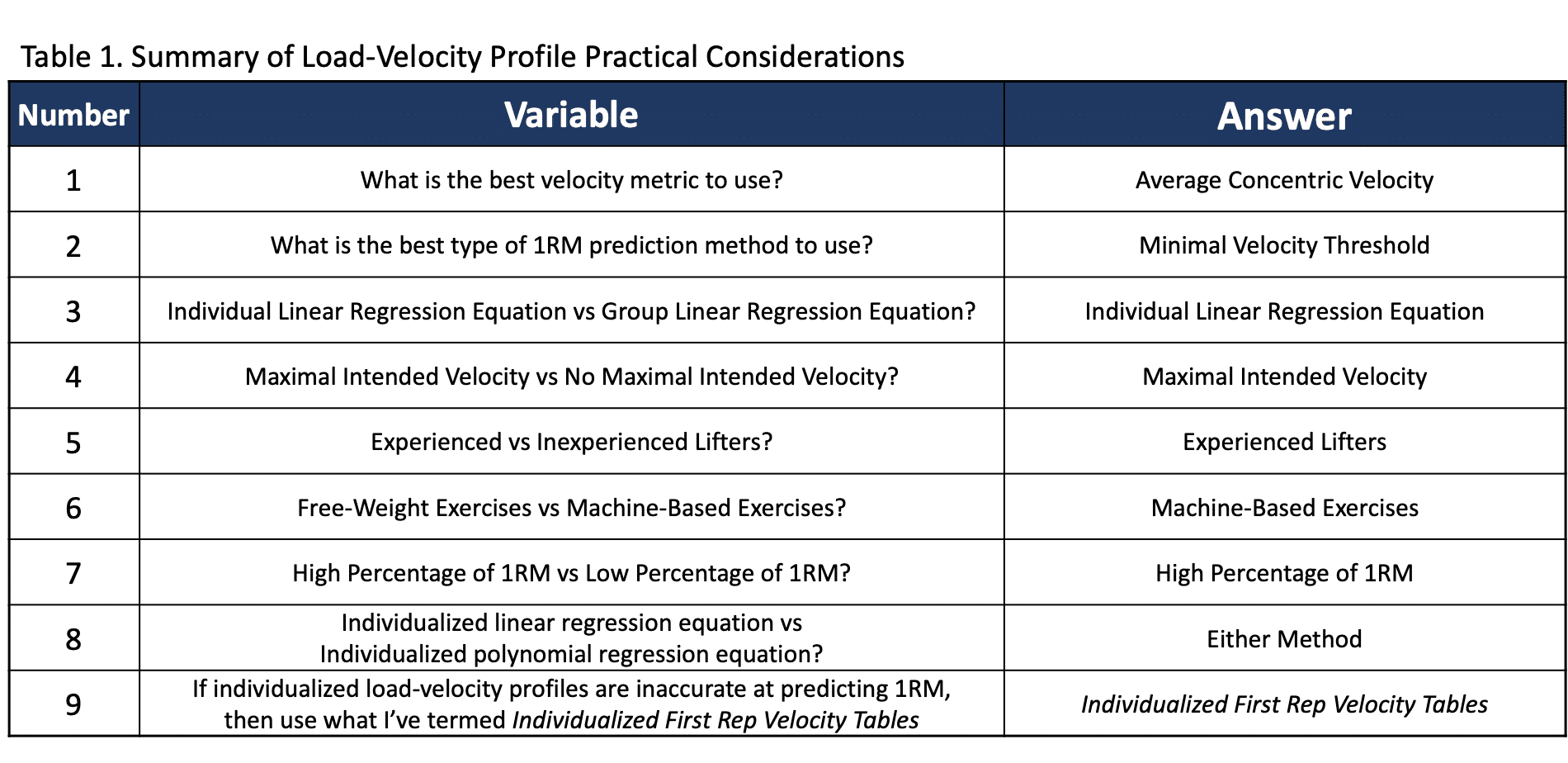
Riassumendo, se sei interessato a provare le equazioni di regressione, dovresti usare un’equazione individualizzata (prova sia lineare che polinomiale), ACV come metrica della velocità, MVT come metodo di previsione, un segnale di velocità massima prevista e un alto percentuale di 1RM. Inoltre, la previsione potrebbe essere più accurata se sei di uno stato di allenamento più alto e lo stai usando per un esercizio basato su macchina (cosa che probabilmente è rara). Un riassunto delle considerazioni pratiche è illustrato nella tabella 1.

Una domanda finale potrebbe essere: “Nella letteratura, quanto sono accurate le profili di carico-velocità nella previsione del 1RM?”. Alcuni sono quasi perfetti (5, 8), mentre altri sovrastimano il 1RM fino a circa 25 chili (6, 7), ma è in gran parte variabile tra individui. Tuttavia, la buona notizia è che la velocità è affidabile a ogni percentuale di 1RM (11). Pertanto, di solito suggerisco l’utilizzo di ciò che ho definito una Tabella delle velocità di prima ripetizione individualizzata e la cross-referenziazione della velocità con la percentuale di 1RM. Come nota finale, personalmente penso che la previsione del 1RM sia più utile come strumento per monitorare il 1RM nel tempo piuttosto che come metodo effettivo per prescrivere TUTTA la sessione, semplicemente perché altre strategie di autoregolazione possono prescrivere e autoregolare in modo appropriato il carico e il volume. Il prossimo articolo affronterà i metodi di previsione e monitoraggio del 1RM che ho trovato efficaci utilizzando la Tabella di Velocità del Primo Ripetuto Individualizzata che ho creato.

Punti chiave

1. Considerazioni per i profili di carico-velocità includono l’utilizzo di una equazione individuale, velocità concentrica media, soglia di velocità minima, velocità massima intenzionale e un alto percentuale di 1RM
2. Utilizzare equazioni di regressione lineare individualizzate o equazioni polinomiali di secondo ordine individualizzate solo se sono accuratamente coerenti nella previsione del 1RM per te
3. Utilizzare ciò che ho definito una Tabella di Velocità del Primo Ripetuto Individualizzata per fare riferimento alla velocità del primo ripetuto individualizzato con la percentuale individualizzata di 1RM come metodo rapido ed efficace per determinare accuratamente la percentuale di 1RM sulla barra e prevedere 1RM.

Riferimenti

1. Garcia-Ramos, A, Pestana-Melero, FL, Perez-Castilla, A, Rojas, FJ, and Haff, GG. Mean velocity vs. mean propulsive velocity vs. peak velocity: which variable determines bench press relative load with higher reliability. The Journal of Strength and Conditioning Research 32(5), 1273 – 1279, 2018.
2. Hughes, LJ, Banyard HG, Dempsey, AR, and Scott, BR. Using a load-velocity relationship to predict one repetition maximum in free-weight exercise: a comparison of the different methods. The Journal of Strength and Conditioning Research 33(9), 2409 – 2419, 2019.
3. Benavides-Ubric, A, Diez-Fernandez, DM, Rodriguez-Perez, MA, Ortega-Becerra, M, and Pareja-Blanco, F. Analysis of the load-velocity relationship in deadlift exercise. Journal of Sports Science and Medicine 19, 452 – 459, 2020.
4. Helms, ER, Storey, AG, Cross, MR, Brown, SR, Lenetsky, S, Ramsay, H, Dillen, C, and Zourdos, MC. RPE and velocity relationships for the back squat, bench press, and deadlift in powerlifters. The Journal of Strength and Conditioning Research 31(2): 292 – 297, 2017.
5. Jimenez-Alonso, A, Garcia-Ramos, A, Cepero, M, Miras-Moreno, S, Rojas, FJ, and Perez-Castilla. Velocity performance feedback during the free-weight bench press testing procedure: an effective strategy to increase the reliability and one repetition maximum accuracy prediction. The Journal of Strength and Conditioning Research [Epub ahead of print], 2020.
6. Banyard, HG, Nosaka, K, and Haff, GG. Reliability and validity of the load-velocity relationship to predict the 1RM back squat. The Journal of Strength and Conditioning Research 31(7), 1897 – 1904, 2017.
7. Ruf, L, Chery, C, and Taylor K. Validity and reliability of the load-velocity relationship to predict the one-repetition maximum in deadlift. The Journal of Strength and Conditioning Research 32(3), 681 – 689, 2018.
8. Perez-Castilla, A, Suzovic, D, Domanovic, A, Fernandes, JFT, and Garcia-Ramos, A. Validity of different velocity-based methods and repetitions-to-failure equations for predicting the 1 repetition maximum during 2 upper-body pulling exercises. The Journal of Strength and Conditioning Research [Epub ahead of print], 2019.
9. Pestana-Melero, FL, Haff, GG, Rojas, FJ, Perez-Castilla, A, and Garcia-Ramos, A. Reliability of the load-velocity relationship obtained through linear and polynomial regression models to predict the 1-repetition maximum load. Journal of Applied Biomechanics 34(3), 184 – 190.
10. Dorrell, HF, Moore, JM, and Gee, TI. Comparison of individual and group-based load-velocity profiling as a means to dictate training load over a 6-week strength and power intervention. Journal of Sports Sciences [Epub ahead of print].
11. Banyard, HG, Nosaka, K, Vernon, AD, and Haff, GG. The reliability of individualized load-velocity profiles. International Journal of Sports Physiology and Performance 13(6), 763 – 769.