Come usare l’allenamento basato sulla velocità e l’analisi dell’inferenza basata sull’ampiezza per monitorare accuratamente il tuo progresso

Uno dei momenti più eccitanti e confortevoli per ogni allenatore sulla Terra è quando i nostri atleti centrano un PR. È quasi come se stessimo compiendo noi stessi e la sensazione di “il mio lavoro sta dando i suoi frutti” è il pasto perfetto per nutrire il nostro ego.

Ma, se ti dicessi che c’è una possibilità che tu stia interpretando il vero progresso del tuo atleta in modo errato?

Due anni fa, durante un corso di statistica per il mio master, stavamo parlando di come interpretare i risultati dei test e di analizzare diversi set di dati. Uno degli esercizi consisteva nell’analizzare la differenza tra alcuni pre e post-test, interpretarli, presentare un rapporto e condividerlo con il resto della classe. Sembrava un compito abbastanza semplice e facile, in realtà troppo facile. Ho completato l’attività utilizzando una semplice analisi che mostrava il % di cambiamento individuale e lo confrontava con la media del gruppo. Fino a questo punto tutto bene.

Tuttavia, il semplice compito era nient’altro che una trappola per il professore. Non appena ha rivisto uno dei rapporti, ha detto una delle più potenti citazioni che abbia mai sentito e quella che ha cambiato il mio atteggiamento verso le statistiche, passando dall’odio puro all’entusiasmo. “Chiunque può essere un grande allenatore con un uso di merda delle statistiche”.

In breve, il compito era semplicemente una introduzione ad uno dei argomenti statistici più rilevanti, se non il più rilevante, nel campo della scienza dello sport, l’inferenza basata sulla magnitudine (MBI)^1,2.

Consideriamo i risultati ottenuti da una misurazione. Se potessimo effettuare una misurazione “perfetta”, otterremmo il “valore reale”. Tuttavia, la realtà è che le misurazioni che facciamo non sono mai perfette e i valori ottenuti da una misurazione sono quindi stimati su questo “valore reale”. Un valore misurato differirà dal “valore reale” ipotetico per un numero di motivi diversi, alcuni dei quali potremmo conoscere, altri no.

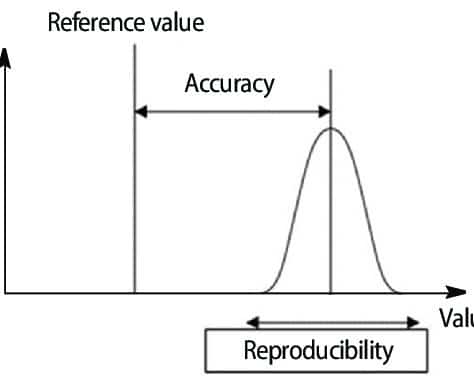Figura 1: Accuratezza e riproducibilità (precisione) di una misurazione. Il valore reale è sempre sconosciuto, ma più la media delle misurazioni si avvicina ad esso, maggiore è l’accuratezza della misurazione³.

 

Chiamiamo la differenza tra un valore misurato e il valore “vero” dell’ERRORE, e più uno è vicino all’altro, più precisa è la nostra misurazione. Per definizione, non possiamo mai conoscere il valore esatto del “vero” e senza di esso, non possiamo nemmeno conoscere la differenza esatta tra esso e le misurazioni che abbiamo effettuato. Quindi, conoscere il valore esatto di un errore è impossibile^3.

Tuttavia, possiamo descrivere l’errore nel risultato di una misurazione specifica come un estrazione da una distribuzione di probabilità. L’incertezza associata a un valore misurato è una misura di quella distribuzione di probabilità. In particolare, l’incertezza standard è lo scarto quadratico medio di questa distribuzione di probabilità. Ciò significa che quanto più variabile è un insieme di dati, maggiore sarà l’incertezza e l’errore.

Tutti sono familiari con i test di RM1, che spesso vengono considerati come lo “standard d’oro” per valutare la capacità di forza degli individui in ambienti non laboratorio⁴

Eseguire un protocollo di test RM è probabilmente più accurato, ma d’altra parte è più time-consuming, faticoso e influenzato da fattori interni (ad esempio, i ritmi circadiani sono stati dimostrati in grado di alterare significativamente le prestazioni ⁵,) e esterni come il feedback verbale dell’allenatore ⁶ o anche la musica.⁷. Inoltre, non possiamo eseguire il test quotidianamente, quindi forse non stiamo rilevando miglioramenti o decrementi a causa del quadro temporale in cui viene applicato il test. Pertanto, stiamo perdendo l’opportunità di aggiustare il piano in tempo.

Al contrario, se stimiamo il valore di 1RM e se scegliamo il metodo appropriato, guadagniamo in praticità, semplicità, tempo e idoneità per periodi di tempo più brevi (giornalieri, settimanali) senza influire negativamente sul normale processo di allenamento, ma a scapito di una maggiore “incertezza” ed “errore”, anche se potremmo davvero, intendo davvero, ridurli.

Se ipotizziamo di testare (o stimare) il 1RM lo stesso giorno con lo stesso atleta senza alcun effetto negativo di un test sugli altri, otterremo 3 valori diversi, una media e una variabilità data (SD). Quindi, la domanda è: come possiamo essere certi che la differenza sia un miglioramento del “segnale” e non la normale variazione dei dati (rumore)?

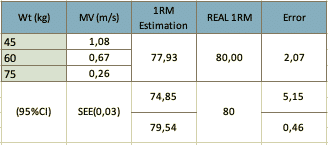
Figura 2: Esempio di stima di 1RM con 3 carichi submassimali e confronto con un test 1RM effettivo. Si noti che la stima è di 2,07 kg in meno rispetto all’1RM effettivo e con un IC del 95% la differenza varia tra 5,15 e 0,46 kg. Non tenerne conto potrebbe generare interpretazioni e decisioni fuorvianti.

Stima del RM 1 utilizzando VBT

I giorni di test sono un po’ alle nostre spalle, escludendo gli sport di forza (ma anche qui). Gli allenatori di oggi non possono permettersi di dedicare un’intera giornata al test, soprattutto negli sport di squadra che si svolgono ogni fine settimana. Ma l’essenza del test è monitorare sia il carico di allenamento che gli effetti dell’allenamento senza influire negativamente sul normale processo di allenamento, aiutandoci a modificare il processo di allenamento se necessario⁸.

In passato, anche se esisteva l’allenamento basato sulla velocità (VBT), veniva utilizzato solo per la ricerca principalmente a causa dei costi dei dispositivi. Ma, nell’ultimo decennio, la rapida diffusione e l’aumento dell’accessibilità dei trasduttori lineari hanno contribuito alla realtà di oggi, dove praticamente ogni allenatore di forza aggiornato include il VBT nei suoi programmi.

L’utilizzo di VBT è stato dimostrato essere un modo veramente preciso per stimare 1RM a causa della relazione matematica lineare e stabile (inversamente correlata, con coefficienti di correlazione> > 0,95) che esiste tra il carico e la velocità concentrica media a cui viene spostato quel carico^9,10, almeno altrettanto buono come il metodo di ripetizione all’insuccesso¹⁰. Inoltre, il metodo a due punti è emerso di recente come una procedura valida, fattibile, veloce e priva di fatica per la valutazione sia della relazione forza-velocità che della relazione carico-velocità, che devono eseguire solo 2 diversi carichi esterni rappresentanti circa il 50% e l’80% di 1RM dichiarato per ottenere un profilo L-V^11-13.

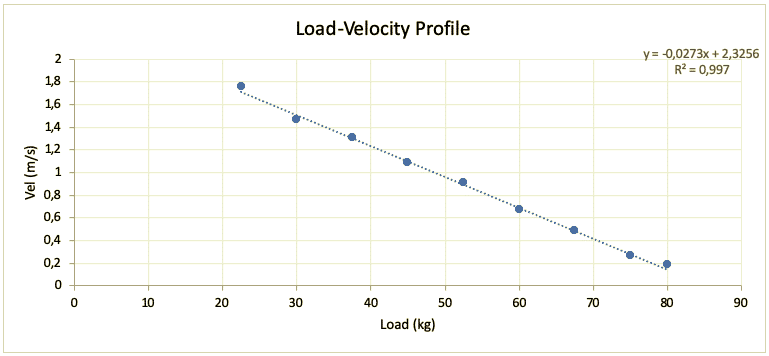Figura 3: Esempio di profilo L-V in Bench Press eseguito da un giocatore di rugby giovanile (misurato tramite dispositivo Vitruve).

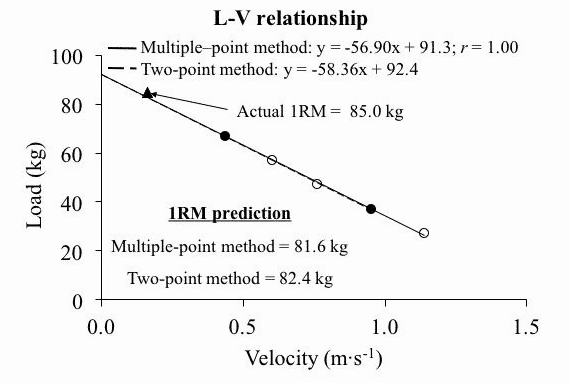Figura 4: metodo a due punti per la valutazione del profilo L-V García Ramos, Amador & Jaric, Slobodan, (2017) ¹¹.

Tuttavia, alcune cose devono essere considerate:

1. Gli esercizi tradizionali come squat, pressa da banco, stacco da terra, ecc. Hanno il proprio profilo di carico-velocità (L-V). Ciò significa che dobbiamo stabilire il profilo L-V per un dato atleta e esercizio prima di stimarlo con carichi submassimali quotidiani.⁹.
2. La relazione L-V è più sensibile alla velocità media o alla velocità media propulsiva che alla velocità massima negli esercizi tradizionali ^10.
3. Il dispositivo deve essere valido e affidabile.¹⁴.
4. I tentativi di carico massimo sono associati a una velocità specifica che è nota come “soglia di velocità minima (MVT)”. ¹⁵ Questo significa che la velocità media del 1RM non sarà significativamente diversa, dal punto di vista statistico, dalla velocità media dell’ultima ripetizione di un determinato RM (5RM, 3RM, ecc.). Ci sono molti studi su diversi esercizi e sui loro MVT (ad esempio, la pressione della banca e dello squat sono solitamente di 0,13-0,3 m / s rispettivamente) ^16,17
5. I percentuali relativi maggiori sono migliori predittori del RM attuale rispetto a quelli inferiori. ^11. Il carico di 5 RM è meno preciso di quello di 3 RM per stimare il RM.

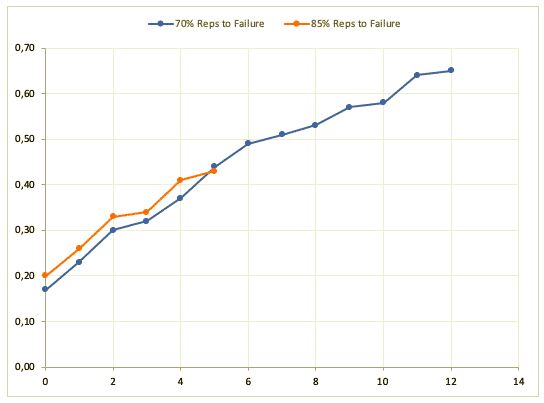Figura 5: Esempio di comportamento lineare e MVT raggiunti per un dato numero di ripetizioni fino al cedimento eseguite con 70% e 85% 1RM (misurato tramite dispositivo Vitruve).

Una volta che conosciamo il profilo L-V per un dato atleta e un dato esercizio, nonché il MVT, siamo pronti a partire!

Inferenza basata sulla magnitudine

MBI si basa sul lavoro dei professori William Hopkins e Alan Batterham ¹⁸ e cerca di correggere alcuni aspetti negativi che l’utilizzo di approcci statistici tradizionali potrebbe generare, aiutando così a identificare le differenze e ottimizzare il processo decisionale.

Gli scienziati dello sport e gli allenatori di solito lavorano con piccoli gruppi di atleti per raccogliere e analizzare i dati, come nello sport di squadra, e anche con N = 1, come nella sollevamento pesi, atletica leggera e anche nello sport di squadra in cui l’analisi dei cambiamenti individuali nel tempo diventa cruciale. Inoltre, a volte, piccoli cambiamenti valgono la pena anche se le differenze non sono rilevanti dal punto di vista statistico (quanti millisecondi separano il vincitore dal perdente in una finale di 100 metri alle Olimpiadi, o cm nel lancio del peso o kg in una gara di sollevamento pesi o di pesi). informazioni utili. Le statistiche tradizionali non funzionano bene né con piccoli N né con minuscole differenze per fornire.

Uno dei pilastri della MBI è la definizione del più piccolo cambiamento praticamente significativo, o il più piccolo cambiamento utile (SWC). Ma prima è cruciale comprendere cosa sia davvero il cambiamento.

Il cambiamento è strettamente collegato al concetto di differenza, ovvero il cambiamento viene giudicato sulla base di una differenza in una determinata entità e riguarda quasi sempre un periodo di tempo³. Ad esempio, se a seguito di un allenamento, un atleta aumenta il suo 1RM da 110 a 150 in 6 settimane, questo verrà considerato un cambiamento positivo. Il principio fondamentale è che le misurazioni della stessa variabile differiscono da una sessione di test all’altra quando sono estese su giorni o settimane. Tuttavia, come già discusso, ci troviamo di fronte a molta incertezza, soprattutto quando le differenze non sono così grandi.

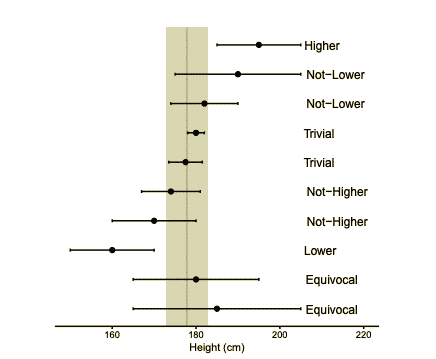Figura 6: Il punto nero rappresenta la media di un determinato test; le righe CI (errore); La linea verticale è la media del gruppo e l’area grigia è l’SWC¹⁹

 

Quindi, tornando a SWC, considerandolo insieme all’errore tipico di un test (TE), ci può aiutare a determinare se il cambiamento di una determinata variabile è reale (segnale) o fa parte della variabilità normale (distribuzione) della misurazione (rumore).

Dobbiamo tenere in considerazione 3 punti quando calcoliamo la SWC per un singolo individuo:

• La percezione, basata sull’esperienza, può essere utilizzata per la SWC. Ad esempio, nel test IMTP, i cambiamenti di meno di 5N sono probabilmente solo rumore.
• L’errore di misurazione è cruciale per identificare il segnale e il rumore. Ad esempio; se il TE è 5N per l’IMTP, SWC non può essere inferiore a due volte quel valore, altrimenti l’incertezza è troppo grande per differenziare i veri cambiamenti e la variabilità.
• Se testiamo un gruppo di atleti, possiamo moltiplicare 0,2 per gli atleti SD per ottenere SWC e 0,3 se il set di dati è preso da un singolo individuo più test.

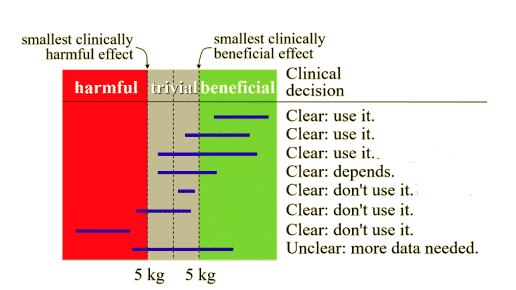
Figura 7: Le decisioni nell’inferenza basata sulla magnitudo vengono prese in base agli intervalli di confidenza o alla distribuzione (linee orizzontali blu) in relazione a un SWC (linee verticali tratteggiate su ciascun lato dell’area banale). Per esempio; Qualsiasi aumento o diminuzione su un 1RM di un atleta superiore a 5 kg è considerato rilevante, mentre tutti i cambiamenti inferiori a 5 kg sono troppo piccoli per essere di rilevanza pratica (cioè banali). Man mano che l’intervallo di confidenza (distribuzione) si allontana dalla zona banale (verso un’area benefica o dannosa), aumenta la probabilità di un vero effetto^20.

Applicazioni pratiche:

Abbiamo ora un modo per stimare il nostro RM degli atleti che può essere implementato anche negli set di riscaldamento. Utilizzando i pesi sub-max e la velocità concentrica di monitoraggio, possiamo creare un metodo in cui possiamo tracciare il nostro RM su base giornaliera senza affaticamento, sprecare tempo e influenzare la sessione di allenamento. Mescolando con MBI può essere un modello potente in grado di fornirci preziose informazioni sulla probabilità di migliorare o diminuire il nostro RM senza nemmeno testarlo.

La seguente immagine è tratta da un foglio di calcolo di Mladen Jovanovic. Questo intero post sul blog è ispirato al suo lavoro. Consiglio vivamente a tutti di seguire il suo lavoro perché è probabilmente (non calcolato MBI) uno dei più dirompenti, innovativi e utili nel campo.

Figure 8: Tracciamento giornaliero dell’1RM utilizzando VBT da 1 Set di peso fisso utilizzando il numero di ripetizioni più veloce mischiato con MBI per stimare la probabilità di cambiamento in 1 anno. I punti blu rappresentano i punti dati con le barre di errore; La linea grigia è la linea di base e l’area grigia rappresenta SWC. La linea verde rappresenta la probabilità di un effetto dannoso espresso in %. Le frecce verdi rappresentano i momenti in cui le probabilità di benefici reali sono elevate e le frecce rosse i momenti in cui le probabilità di danni reali sono le più elevate.

L’utilizzo di questo approccio può aiutare sia nell’valutare l’effetto di diversi aspetti dell’allenamento, come il volume, la frequenza, la densità e il carico sull’«outcome» (1RM), sia come strumento di preparazione.

 

 

Bibliografia

1. Hopkins, W. G. Magnitude Matters. Medicine & Science in Sports & Exercise 38, 56 (2006).
2. Batterham, A. M. & Hopkins, W. G. The Case for Magnitude-based Inference. Medicine & Science in Sports & Exercise 47, 885 (2015).
3. Dvir, Z. Difference, significant difference and clinically meaningful difference: The meaning of change in rehabilitation. J Exerc Rehabil 11, 67–73 (2015).
4. Levinger, I. et al. The reliability of the 1RM strength test for untrained middle-aged individuals. Journal of Science and Medicine in Sport 12, 310–316 (2009).
5. WINGET, C. M., DEROSHIA, C. W. & HOLLEY, D. C. Circadian rhythms and athletic performance. Medicine & Science in Sports & Exercise 17, 498???516 (1985).
6. Argus, C. K., Gill, N. D., Keogh, J. W. & Hopkins, W. G. Acute Effects of Verbal Feedback on Upper-Body Performance in Elite Athletes. Journal of Strength and Conditioning Research 25, 3282–3287 (2011).
7. Loizou, G. & Karageorghis, C. I. Effects of psychological priming, video, and music on anaerobic exercise performance. Scand J Med Sci Sports 25, 909–920 (2014).
8. Clarke, D. C. & Skiba, P. F. Rationale and resources for teaching the mathematical modeling of athletic training and performance. Advances in Physiology Education 37, 134–152 (2013).
9. González-Badillo, J. J. & Sánchez-Medina, L. Movement Velocity as a Measure of Loading Intensity in Resistance Training. Int J Sports Med 31, 347–352 (2010).
10. Jidovtseff, B., Harris, N. K., Crielaard, J.-M. & Cronin, J. B. Using the load-velocity relationship for 1RM prediction. Journal of Strength and Conditioning Research 25, 267–270 (2011).
11. Garcia-Ramos, A. & Jaric, S. Two-Point Method. Strength and Conditioning Journal 40, 54–66 (2018).
12. García-Ramos, A. et al. Feasibility of the 2-Point Method for Determining the 1-Repetition Maximum in the Bench Press Exercise. International Journal of Sports Physiology and Performance 13, 474–481 (2018).
13. Snyder, B. W., Zangakis, D. S., Moir, G. L., Munford, S. N. & Davis, S. E. Validity of the Two-Point Method for Estimating Squat and Bench Press One Repetition Maximums. Medicine & Science in Sports & Exercise 51, 49 (2019).
14. Pérez-Castilla, A., Piepoli, A., Delgado-García, G., Garrido-Blanca, G. & García-Ramos, A. Reliability and Concurrent Validity of Seven Commercially Available Devices for the Assessment of Movement Velocity at Different Intensities During the Bench Press. Journal of Strength and Conditioning Research 33, 1258–1265 (2019).
15. Izquierdo, M. et al. Effect of Loading on Unintentional Lifting Velocity Declines During Single Sets of Repetitions to Failure During Upper and Lower Extremity Muscle Actions. Int J Sports Med 27, 718–724 (2006).
16. Ayllon, F., Larumbe, E., Jiménez, A. & Alvar, B. 1 Rm Prediction From The Linear Velocity And The Rate Of Perceived Exertion In Bench Press And Paralell Squat. Journal of Strength and Conditioning Research 24, 1 (2010).
17. Banyard, H. G., Nosaka, K. & Haff, G. G. Reliability and Validity of the Load–Velocity Relationship to Predict the 1RM Back Squat. Journal of Strength and Conditioning Research 31, 1897–1904 (2017).
18. Batterham, A. M. & Hopkins, W. G. Making Meaningful Inferences About Magnitudes. International Journal of Sports Physiology and Performance 1, 50–57 (2006).
19. Jovanovic, M. Statistical Modelling for Sports Scientists: Practical Introduction Using R (Part 1). (2019). doi:10.31236/osf.io/dnq3m
20. Hooren, B. Magnitude-based inference: What is it? How does it work and is it appropriate? (2018).