Profils de vitesse de prêt individualisés : considérations d’application pour une meilleure précision de prédiction

Les profils de charge-vitesse personnalisés sont couramment utilisés pour prédire le 1RM. Néanmoins, les résultats sont mitigés : certaines études démontrent qu’ils peuvent prédire le 1RM avec précision ; cependant, d’autres études révèlent le contraire. Rejoignez-moi alors que j’aborde quelles sont les subtilités individuelles qui doivent être prises en compte pour une application afin d’augmenter la précision de la prédiction du 1RM.

 

Points clés

1. Les équations de régression linéaire individualisées sont les profils de charge-vitesse les plus couramment employés pour prédire le 1RM.
2. Les conclusions générales de la littérature sont mitigées en termes de précision de la prédiction du 1RM.
3. Il existe plusieurs considérations d’application pour augmenter la précision de la prédiction du 1RM.

Lorsqu’on parle de « Formation basée sur la vitesse », ce qui vient à l’esprit de la plupart des individus est le profil de charge-vitesse. Ensuite, la plupart des individus pensent généralement à une équation de régression impliquant la vitesse sur l’axe des abscisses et la charge sur l’axe des ordonnées avec une extrapolation de la vitesse afin de prédire le 1RM. Les équations de régression sont généralement utilisées pour prédire le 1RM afin de surveiller le 1RM au fil du temps ou comme méthode pour prescrire la séance d’entraînement. Il existe d’innombrables études impliquant des profils de charge-vitesse par équation de régression; par conséquent, plutôt que de traiter chaque étude individuellement, cet aperçu court fournira un bref aperçu des considérations et des subtilités individuelles les plus importantes pour augmenter la précision de la prédiction du 1RM.

Résumé, ces études étudient la validité et/ou la fiabilité des profils de charge-vitesse pour la prédiction de 1RM. La validité se réfère à la précision des méthodes de prédiction de 1RM. La fiabilité se réfère à la cohérence des méthodes de prédiction de 1RM. Il est important d’examiner à la fois la validité et la fiabilité, car une méthode de prédiction de 1RM peut être invalide (ne prédit pas précisément le 1RM), mais elle peut toujours être fiable, ce qui signifie qu’elle surestime ou sous-estime constamment le 1RM d’une magnitude spécifique. Par exemple, disons qu’une certaine méthode de prédiction de 1RM surestime constamment le 1RM de 10 kilos. Bien qu’elle soit invalide (elle surestime le 1RM de 10 kilos), elle est fiable (elle surestime constamment le 1RM de 10 kilos). Par conséquent, dans cet exemple particulier, cette personne pourrait toujours utiliser cette méthode solide pour prédire le 1RM en sachant simplement que son 1RM est toujours ~10 kilos inférieur à la prédiction réelle.

Personnellement, j’ai joué avec des équations de régression linéaire et des équations de régression polynomiale assez souvent pour prédire le 1RM. Pour moi, les deux méthodes tendent à surestimer le 1RM considérablement, ce qui est cohérent avec ce qui est rapporté dans la plupart des littératures. Pour cette raison, je suggère généralement d’utiliser ce que j’ai appelé une table de vitesse du premier répétition individuelle afin de faire référence à votre vitesse de premier répétition individuelle avec votre pourcentage individuel de 1RM pour une détermination précise de quel pourcentage de 1RM est sur la barre et pour une prédiction précise du 1RM. Cependant, pour certains individus, j’ai constaté que les profils de charge-vitesse des équations de régression typiques sont capables de prédire le 1RM avec une précision raisonnable, donc je pense toujours qu’ils valent la peine d’être discutés. Il suffit de garder à l’esprit les considérations importantes illustrées ci-dessous si vous êtes intéressé à les essayer.

Quelle est la meilleure métrique de vitesse à utiliser?

Il existe diverses métriques de vitesse qui peuvent être utilisées pour prédire le RM1: vitesse concentrique moyenne (ACV), vitesse propulsive moyenne (MPV), vitesse de pointe (PV) et nombreuses autres (1). L’ACV est la vitesse moyenne pendant toute la partie concentrique de l’exercice (c’est-à-dire pendant la partie où vous montez ou «vous déplacez vers le haut» dans le squat ou le développé couché). La MPV est la vitesse moyenne à partir de l’initiation de la partie concentrique de l’exercice jusqu’au point où l’accélération de la barre est inférieure à l’accélération de la gravité (cela peut être particulièrement utile pour évaluer le taux de développement de force; également communément appelé RFD). La PV est la vitesse maximale (donc la vitesse de pointe) atteinte pendant la partie concentrique de l’exercice.

Dans une étude très récente visant à déterminer quelle métrique de vitesse pouvait déterminer le chargement relatif du développé couché avec la plus grande fiabilité, l’ACV avait le coefficient de corrélation de Pearson le plus élevé (R = 0,993) et le plus faible erreur standard de l’estimation (SEE = 5,11 – 6,03%) (1). La valeur R mesure la force de la relation entre deux variables (charge et vitesse dans ce cas particulier) et varie de -1,00 à +1,00 (une valeur absolue de 1,00 indiquerait qu’il existe une corrélation parfaite entre la charge et la vitesse). L’SEE représente la précision et illustre la variation autour d’une ligne de régression (plus le SEE est faible, moins la variance et plus la précision de la prédiction est élevée).

Quel est le meilleur type de méthode de prédiction de 1RM à utiliser?

Il existe actuellement trois méthodes principales de prédiction de 1RM utilisant la vitesse qui sont employées dans la littérature scientifique: seuil minimal de vitesse (MVT), charge à zéro vitesse (LD0) et force-vitesse (FV) (2). Le MVT suggère que la dernière répétition avant l’échec est toujours à la même ACV. Par conséquent, la méthode MVT consiste à résoudre l’équation de régression linéaire pour y (1RM) avec le MVT (x). La méthode LD0 est identique à la méthode MVT; cependant, elle consiste à résoudre l’équation de régression linéaire pour une vitesse de 0 m.s-1, au lieu du MVT. La méthode FV consiste à identifier l’interception entre FV et la relation poids-vitesse (dans ce cas, le poids est déterminé en multipliant chacune des charges absolues par l’accélération standard due à la gravité ou 9,81 m.s-1). En conclusion, la méthode de prédiction de 1RM MVT s’est avérée être la plus valide et la plus fiable des trois méthodes mentionnées ci-dessus (2).

Équations de régression linéaire individuelles vs Équations de régression linéaire de groupe

Il ne devrait pas être surprenant que les équations de régression linéaire individuelles soient plus précises pour prédire le 1RM que les équations de régression linéaire de groupe (3), étant donné que la relation entre la charge et la vitesse doit être individualisée (4). Je ne vois pas l’utilité d’enquêter sur les équations de régression linéaire de groupe, ni l’efficacité des équations de régression linéaire de groupe dans les contextes de groupe. Dans les contextes de groupe, même si plusieurs athlètes utilisent le même dispositif VBT, chaque athlète individuel peut toujours avoir son équation de régression linéaire individuelle (qui dépend de la session; puisque l’équation changera bien sûr chaque session en fonction de la charge exacte et de la vitesse exacte correspondante). Bien sûr, utilisez votre propre profil de charge-vitesse individualisé; ne pas utiliser un profil de charge-vitesse de groupe générique.

Vitesse Intentionnelle Maximale vs Pas de Vitesse Intentionnelle Maximale

Je pense qu’une des principales limitations des études est qu’une indication de vitesse maximale n’est presque jamais fournie. Cependant, dans une étude dans laquelle il y avait une condition qui recevait une indication de vitesse maximale et une condition de contrôle (aucune indication de vitesse maximale n’était reçue), la prédiction du 1RM était légèrement plus précise dans la condition qui recevait une indication de vitesse maximale (erreurs absolues : 3,1 ± 2,3 contre 4,1 ± 1,9 kg) (5). Logiquement, cela ne devrait pas surprendre, car si un sujet n’est pas fourni avec un indice pour soulever chaque répétition avec une vitesse maximale, certaines répétitions peuvent être plus rapides que d’habitude et certaines répétitions peuvent être plus lentes que d’habitude. Par conséquent, cela aura des changements drastiques à la pente de la droite de régression ; par conséquent, influençant le 1RM prédit.

Expérimentés vs Inexpérimentés

Intéressamment, Banyard et al. (2017) ont rapporté que les statuts d’entraînement plus élevés (sujets capables de faire un soulevé de poids libre de 1,5 fois leur masse corporelle) avaient des prédictions de 1RM plus précises que celles des statuts d’entraînement inférieurs (6). Les auteurs n’ont fourni aucune discussion ou interprétation pour expliquer ces résultats. Je ne suis pas entièrement sûr de la raison de cela car j’ai constaté des résultats mixtes chez ceux qui ont un « statut d’entraînement plus élevé ». Pour spéculer, cela peut être dû au fait que les « statuts d’entraînement plus élevés » peuvent « grinder » (c’est-à-dire effectuer des répétitions à des vitesses plus lentes); cependant, étant donné que l’équation de régression linéaire individualisée prend en compte la VMA 1RM individuelle, cela n’explique pas toute l’image.

Exercices à poids libre vs Exercices sur machines

Enfin, nous arrivons aux exercices à poids libre vs exercices sur machines. C’est là que les différences dans les résultats commencent vraiment à se faire sentir. Dans l’ensemble, les équations de régression linéaire impliquant des exercices à poids libre ne sont pas valides (6, 7) ni fiables (6), et surestiment généralement le 1RM réel d’une magnitude significative (6, 7). Cependant, dans l’ensemble, les équations de régression linéaire impliquant des exercices sur machine sont généralement raisonnablement valides et fiables pour la prédiction du 1RM (5, 8). Je ne suis pas entièrement sûr de la raison pour laquelle les exercices sur machine sont généralement plus précis, mais pour spéculer, je pense que cela peut être dû au fait que les exercices à poids libre sont plus sujets aux déviations techniques; ainsi, le parcours distinct de la barre peut jouer un rôle.

Haute pourcentage de 1RM vs faible pourcentage de 1RM.

Les équations de régression linéaire qui utilisent un pourcentage plus élevé de 1RM (~ 80% de 1RM) sont plus précises que celles qui utilisent un pourcentage plus faible de 1RM (~ 60% de 1RM), quel que soit le nombre de points de données impliqués dans l’équation de régression linéaire (6, 7). Par conséquent, il semble que la relation entre la charge et la vitesse devienne courbe (plutôt que linéaire) à mesure que la charge sur la barre augmente. À mon avis, la relation charge-vitesse ressemble davantage à une équation de régression polynomiale de deuxième ordre qu’à une équation de régression linéaire.

Équations de régression linéaire individualisées vs Équations de régression polynomiales individualisées

Je ferais avec prudence l’argument que les équations de régression polynomiales peuvent être plus précises que les équations de régression linéaire pour prédire le 1RM (9), mais malheureusement il y a très peu de recherches sur leur efficacité. Je suis en fait surpris que ce soit le cas, car la composante la plus longue d’une étude est généralement la collecte de données. En d’autres termes, les chercheurs ont déjà les données, il suffit donc de lancer les statistiques, de signaler les résultats et d’intégrer les résultats dans la section discussion du document. En fait, le plus récent document sur la prescription de charge autorégulée a effectivement utilisé une méthode intéressante pour prescrire la charge à l’aide d’une équation de régression polynomiale (10).

 

 

Conclusion

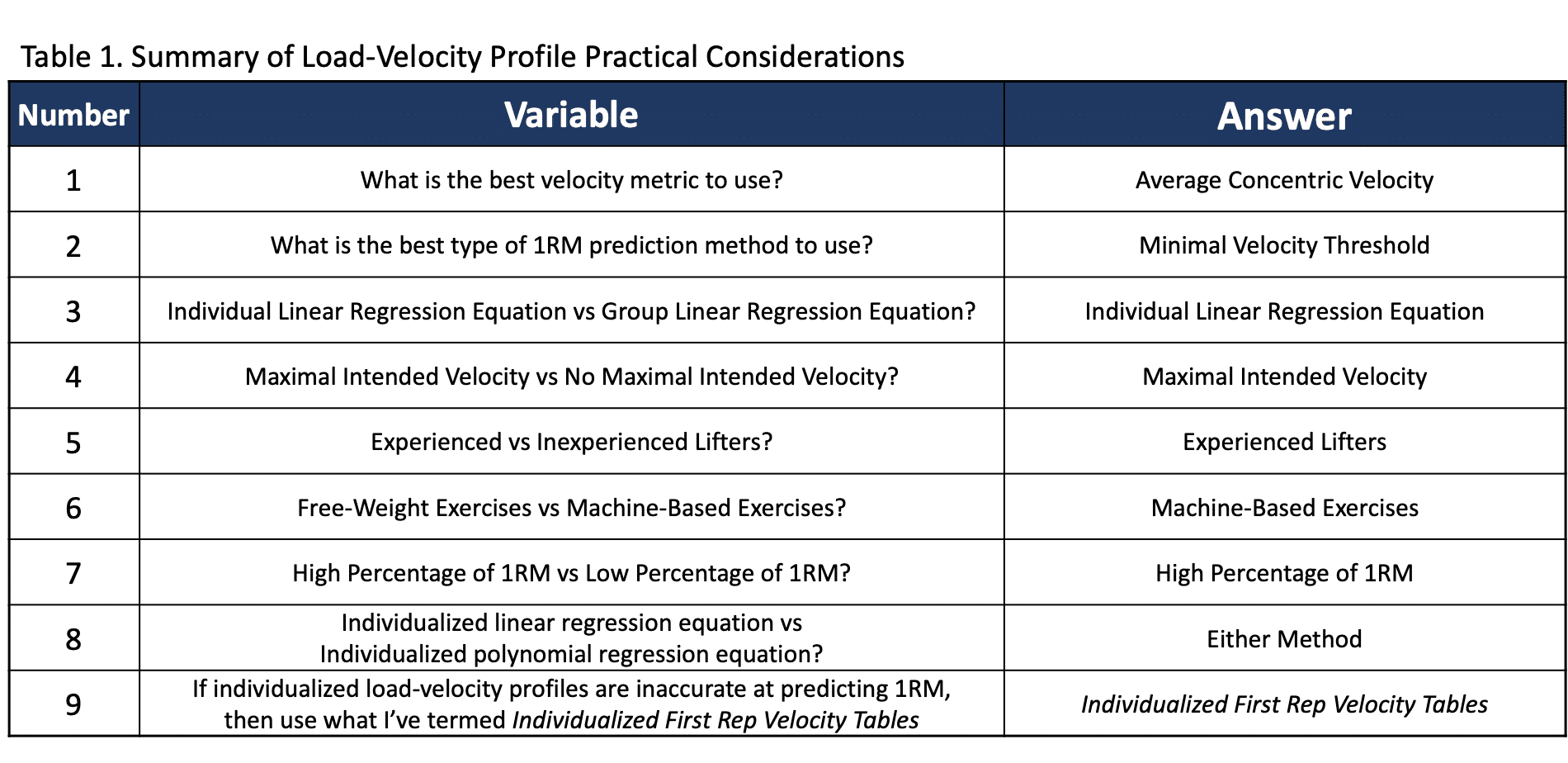
Résumons-nous, si vous êtes intéressé à essayer des équations de régression, vous devriez utiliser une équation individualisée (essayez à la fois linéaire et polynomiale), ACV comme métrique de vitesse, MVT comme méthode de prédiction, un indice maximal de vitesse prévu et un pourcentage élevé de 1RM. De plus, la prédiction peut être plus précise si vous êtes d’un statut d’entraînement plus élevé et que vous l’utilisez pour un exercice basé sur une machine (ce qui est probablement rarement le cas). Un résumé des considérations pratiques est illustré dans le tableau 1.

Une dernière question peut être : « Dans la littérature, à quel point les profils de charge-vitesse sont-ils précis pour prédire le 1RM ? » Certains sont presque parfaits (5, 8), tandis que d’autres surestiment le 1RM jusqu’à environ 25 kilos (6, 7), mais cela varie beaucoup d’une personne à l’autre. Mais la bonne nouvelle, c’est que la vitesse est fiable à chaque pourcentage du 1RM (11). Par conséquent, je suggère généralement d’utiliser ce que j’ai appelé une tableau de vitesse de première répétition individualisé et de faire une comparaison entre la vitesse et le pourcentage du 1RM. Enfin, je pense personnellement que la prédiction du 1RM est plus utile comme outil pour surveiller le 1RM dans le temps plutôt que comme méthode pour prescrire TOUTE la séance, car d’autres stratégies d’autorégulation peuvent prescrire et autoréguler la charge et le volume de manière appropriée. Le prochain article abordera les méthodes de prédiction et de surveillance du 1RM que j’ai trouvées efficaces en utilisant la Table de vitesse du premier répétition individuelle que j’ai créée.

Points clés à retenir

1. Considérations d’application pour les profils de charge-vitesse comprennent l’utilisation d’une équation individuelle, la vitesse concentrique moyenne, le seuil de vitesse minimal, la vitesse prévue maximale et un pourcentage élevé de 1RM
2. Employez des équations de régression linéaire individuelles ou des équations polynomiales du second ordre individuelles uniquement si elles sont constamment précises pour prédire le 1RM pour vous
3. Employez ce que j’ai appelé une table de vitesse de première répétition individuelle afin de faire une référence croisée entre la vitesse de première répétition individuelle et le pourcentage individuel de 1RM comme une méthode rapide et facile pour déterminer avec précision le pourcentage de 1RM sur la barre et prédire le 1RM.

Références

1. Garcia-Ramos, A, Pestana-Melero, FL, Perez-Castilla, A, Rojas, FJ, and Haff, GG. Mean velocity vs. mean propulsive velocity vs. peak velocity: which variable determines bench press relative load with higher reliability. The Journal of Strength and Conditioning Research 32(5), 1273 – 1279, 2018.
2. Hughes, LJ, Banyard HG, Dempsey, AR, and Scott, BR. Using a load-velocity relationship to predict one repetition maximum in free-weight exercise: a comparison of the different methods. The Journal of Strength and Conditioning Research 33(9), 2409 – 2419, 2019.
3. Benavides-Ubric, A, Diez-Fernandez, DM, Rodriguez-Perez, MA, Ortega-Becerra, M, and Pareja-Blanco, F. Analysis of the load-velocity relationship in deadlift exercise. Journal of Sports Science and Medicine 19, 452 – 459, 2020.
4. Helms, ER, Storey, AG, Cross, MR, Brown, SR, Lenetsky, S, Ramsay, H, Dillen, C, and Zourdos, MC. RPE and velocity relationships for the back squat, bench press, and deadlift in powerlifters. The Journal of Strength and Conditioning Research 31(2): 292 – 297, 2017.
5. Jimenez-Alonso, A, Garcia-Ramos, A, Cepero, M, Miras-Moreno, S, Rojas, FJ, and Perez-Castilla. Velocity performance feedback during the free-weight bench press testing procedure: an effective strategy to increase the reliability and one repetition maximum accuracy prediction. The Journal of Strength and Conditioning Research [Epub ahead of print], 2020.
6. Banyard, HG, Nosaka, K, and Haff, GG. Reliability and validity of the load-velocity relationship to predict the 1RM back squat. The Journal of Strength and Conditioning Research 31(7), 1897 – 1904, 2017.
7. Ruf, L, Chery, C, and Taylor K. Validity and reliability of the load-velocity relationship to predict the one-repetition maximum in deadlift. The Journal of Strength and Conditioning Research 32(3), 681 – 689, 2018.
8. Perez-Castilla, A, Suzovic, D, Domanovic, A, Fernandes, JFT, and Garcia-Ramos, A. Validity of different velocity-based methods and repetitions-to-failure equations for predicting the 1 repetition maximum during 2 upper-body pulling exercises. The Journal of Strength and Conditioning Research [Epub ahead of print], 2019.
9. Pestana-Melero, FL, Haff, GG, Rojas, FJ, Perez-Castilla, A, and Garcia-Ramos, A. Reliability of the load-velocity relationship obtained through linear and polynomial regression models to predict the 1-repetition maximum load. Journal of Applied Biomechanics 34(3), 184 – 190.
10. Dorrell, HF, Moore, JM, and Gee, TI. Comparison of individual and group-based load-velocity profiling as a means to dictate training load over a 6-week strength and power intervention. Journal of Sports Sciences [Epub ahead of print].
11. Banyard, HG, Nosaka, K, Vernon, AD, and Haff, GG. The reliability of individualized load-velocity profiles. International Journal of Sports Physiology and Performance 13(6), 763 – 769.